Im Wikipedia-Eintrag zur Tetraktys (Stand Juli 2016) wird der Unterpunkt „Antike Bedeutung“ eingeleitet mit: „Als Tetraktys bezeichneten die Pythagoreer die Gesamtheit der Zahlen 1, 2, 3 und 4, deren Summe 10 ergibt.“

Der Harmoniker Hans Kayser hatte zu diesem Thema eine andere Meinung. In einem Briefwechsel an einem Freund schreibt er: „Diese Vierzahl wird immer mit 1 + 2 + 3 + 4 = 10 bezeichnet, was nur für die Dummen berechnet war. 6, 8, 9, 12 vereinigt jedoch die arithmetische, geometrische und harmonische Proportion in sich, also das Ordnungsgefüge der damaligen Welt“. (Zitat aus dem Büchlein „Das Geheimnis der pythagoräischen Tetraktys“ von Theo Reiser aus dem Jahre 1967.

Über konkrete Einzelheiten der sogenannten Tetraktys = Vierheit der Pythagoreer wurde und wird also vieles behauptet und gemutmaßt. Sowohl im entsprechenden Wikipedia-Eintrag als auch anderswo – unter anderem auch auf meiner Seite tetraktys.de – findet man die Palette bedeutsamer Vierheiten mehr oder weniger vollständig aufgelistet. Da stellt sich natürlich die Frage, was genau nun davon der Wahrheit entspricht.

Auf der Suche nach relevanten Antworten kommt man allerdings an genau zwei antiken Quellen nicht vorbei. Das sind zum einen die Fragmente des Pythagoreers Philolaos. Darin findet man unter anderem folgende Aussage:

„Man muß die Leistungen und das Wesen der Zahl
nach der Kraft bemessen, die in der Zehnzahl liegt.
Denn groß und vollkommen vollendet
und alles bewirkend
und göttlichen und himmlischen
sowie menschlichen Lebens Anfang
sowie Anteil nehmende Führerin ist die Kraft
der Zahl und der Zehn.
Denn ohne diese ist alles unbegrenzt
und undeutlich und unklar“

Des weiteren fällt dem aufmerksamen Leser eine Textpassage eines antiken Buches mit dem Titel „Von den pythagoreischen Zahlen“ auf, welches in verschiedenen Fragmentesammlungen der Vorsokratiker auftaucht und zitiert wird. Der Inhalt dieses Buch soll nach übereinstimmender Quellenlage zufolge ebenfalls von Philolaos selbst stammen. Aufgeschrieben wurde es von Speusippos, dem Sohn von Platons Schwester.

Aus diesem Text geht hervor, was die Pythagoreer an der Menge 10 so faszinierte nämlich, dass alle möglichen Teilereigenschaften zum ersten Mal in der „Zehnzahl“ enthalten sind. Die Rede ist von den „ersten und unzusammengesetzten“ und den „zweiten und zusammengesetzten“. Wie ist das zu verstehen? Nicht ohne die entsprechende Geometrie. Wenn man Zahlenmengen als Polygone und Sternpolygone darstellt, so lässt sich erkennen, dass den 3 bzw. 4 Teilereigenschaften von Mengen auch 4 Typen von Polygonen und Sternpolygonen zugewiesen sind, hier direkt am Beispiel des 10-Ecks:

Des weiteren ist von den geraden Zahlen als „die schließenden Zahlen“ die Rede. Wie ist das zu verstehen? Nicht ohne die entsprechende Geometrie. Geradzahlige Polygone schließen mit der Innenwinkelsumme voller Kreise ab, während ungerade Zahlen mit einem halben Kreis (neuer Eckpunkt = Dreieck von 180 Grad) beginnen.

Der erhalten gebliebene Text dieses Buches „Von den pythagoreischen Zahlen“ ist ier zu finden. Ebenso die Beschreibung zur geometrischen Entsprechung.http://tetraktys.de/einfuehrung-6.html#quellmaterial-tetraktys

Was macht diesen Sachverhalt in Bezug auf die Harmonik eigentlich so erwähneswert? Nun:

All diese Teilereigenschaften von Mengen, dargestellt als Sternpolygone finden sich in einer interessanten „Drehmatrix“ im wichtigsten Diagramm der Harmoniker, dem Lambdoma wieder. Das dabei entstehende Muster entspricht der Darstellung von physikalischen Wellen. Auch die Gleichtonlinien der „harmonikalen Tetraktys“ von Hans Kayser, also 6, 8, 9, 12  bzw. 1/2, 2/3, 3/4, entsprechen der Darstellung von Punkt, Linie, Dreieck und Quadrat innerhalb dieser Matrix. Also 1+2+3+4. Somit schließt sich der harmonikale Kreis.

Ein weiterer interessanter Aspekt dieser Thematik ist die Tatsache, dass etlichen Polygonen und Sternpolygonen von der Antike ausgehend über die Renaissance bis heute eine wichtige symbolische Bedeutung zukommt. Die Einbettung in eine stringente und komplexe Systematik wie eben dem Lambdoma bzw. der Divisionstabelle erlaubt demnach detaillierte Aussagen über das jeweilige Symbol auf wissenschaftlich fundierter Grundlage.

Exemplarisch für diese Betrachtungsweise steht das Pentagramm, als Erkennungszeichen der Pythagoreer, welches als „Doppelpentagramm“ zum ersten Mal als die dritte und letzte Teilereigenschaft in der Konstellation 10/4 zu finden ist, siehe die folgende Abbildung: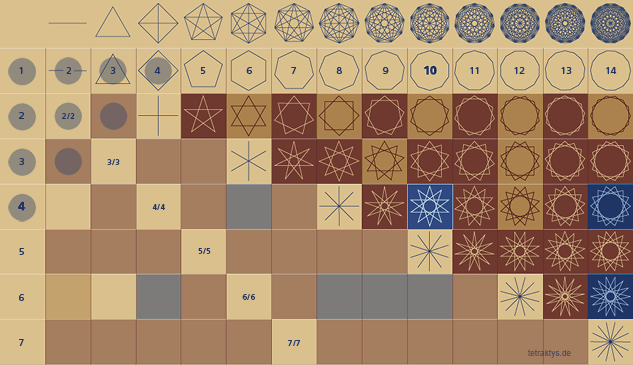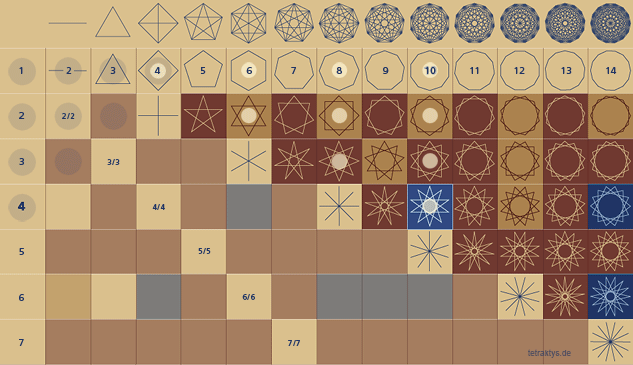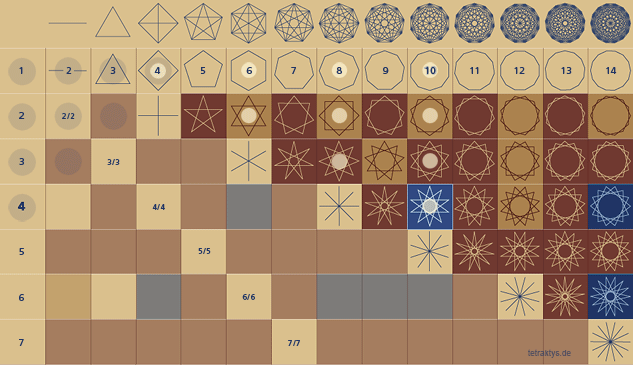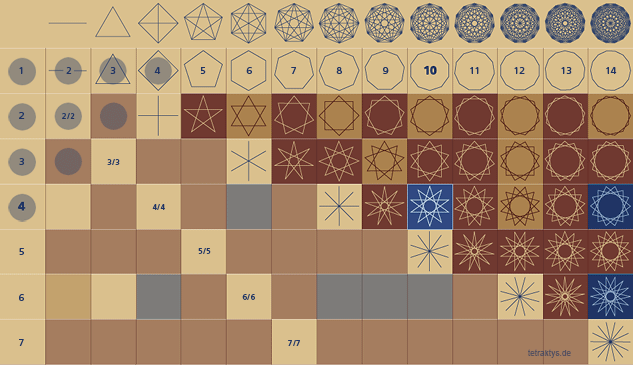

Das Doppelpentagramm, also das aufrechte und das gestürzte Pentagramm symbolisiert den Menschen in der Materie, ebenso das Viereck mit dem Kreuz und seinem Mittelpunkt – also 10 geteilt durch 4.

Weitere Einzelheiten sind zu finden auf der Seite tetraktys.de

Eine erweiterte Abhandlung findet sich auch hier als pdf-Datei.