Blog-Archive

Mystik und Harmonik

Eein Beitrag von Willibald Limbrunner

 

Mystik hat heute in aller Regel eine negative Konnotation. Die Definition lt. Wikipedia:

 

Der Ausdruck Mystik (von griechisch μυστικός mystikós ‚geheimnisvoll‘, zu myein ‚Mund oder Augen schließen‘) bezeichnet Berichte und Aussagen über die Erfahrung einer göttlichen oder absoluten Wirklichkeit sowie die Bemühungen um eine solche Erfahrung. https://de.wikipedia.org/wiki/Mystik

 

Im landläufigen Sinne wird „absolute Wirklichkeit“ religiös interpretiert. Der Ausdruck „absolute Wirklichkeit“ würde, so gesehen, eine umfassende Abhandlung der europäischen Geschichte erfordern. Dennoch werden Ergebnisse moderner Forschung heute als „absolute Wirklichkeit“ in Szene gesetzt. Auch das will kritisch hinterfragt werden. Die Mathematik mag wohl noch als Refugium einer Wirklichkeit gesehen werden, die auch heute noch den Rang einer absoluten Wirklichkeit besitzt. Gegen mathematische Regeln ist nichts einzuwenden, denn sie führen zu korrekten Ergebnissen. Dies jedoch nur innerhalb der mathematischen Axiomatik und nicht in Bezug auf die Welt, die wir wahrnehmen. Beide, die Welt der Wahrnehmung und die Mathematik wurden schon vor zweieinhalb tausend Jahren in einer wunderbaren Symbiose miteinander Verbunden.

Pythagoras von Samos gilt heute als der Beginn dieser Symbiose zwischen Mathematik und Welt, zwischen Idee und Wirklichkeit. Pythagoras gilt als Entdecker des Zusammenhangs der Länge einer Saite und ihrem Klang. Heute würden wir das als Zusammenhang zwischen Wellenlänge (Saite) und Frequenz (Klang) sehen wollen. Wir lassen die physikalische Definition des Klanges zunächst vereinfachend beiseite.

Dieser Zusammenhang vereint zwei scheinbar unvereinbare Dinge. Das innerweltliche Erlebnis des Klanges und der physikalisch-mathematische Aspekt der Klangerzeugung. Dabei gelangen wir zu dem, was die Griechen „myein“ nannten, dem „Schließen der Augen“, dem innerweltlichen Erleben einer „absoluten Wirklichkeit“, die uns als das mathematische Längenverhältnis zweier klingender Saiten entgegentritt. Wir haben das, was in der Musik lapidar, Intervallverhältnis genannt wird. Jedoch ist es zutiefst „mystisch“ und wird in der Harmonik Hans Kaysers, „Akroasis“ (Anhörung) genannt.

Ein harmonikales Längenverhältnis lässt sich auf zwei ganze Zahlen zurückführen:

 

„Die ganzen Zahlen hat der liebe Gott gemacht, alles andere ist Menschenwerk.“
Leopold Kronecker

 

Im Mysterium der ganzen Zahl scheint der religiöse Aspekt der Mystik in der Mathematik als absolute Wirklichkeit auf.

Seit der Entdeckung des Planckschen Wirkungsquantums durch Max Planck und die Enträtselung der Atomstruktur ist die pythagoreische Zahlensphilosophie keine Spekulation mehr. Heisenberg schreibt:

 

… seit der berühmten Arbeit von Planck aus dem Jahre 1900 nannte man solche Forderungen Quantenbedingungen. Und diese Bedingungen brachten eben jenes merkwürdige Element von Zahlenmystik in die Atomphysik, von dem vorher schon die Rede war. Gewisse aus der Bahn zu berechnende Größen sollten ganzzahlige Vielfache einer Grundeinheit, nämlich des Planckschen Wirkungsquantums sein. Solche Regeln erinnerten an die Beobachtungen der alten Pythagoreer, nach denen zwei schwingende Saiten dann harmonisch zusammenklingen, wenn bei gleicher Spannung ihre Längen in einem ganzzahligen Verhältnis stehen.
Werner Heisenberg, Der Teil und das Ganze, 8. Aufl., 2010, Piper Verlag, München, S.47.

 

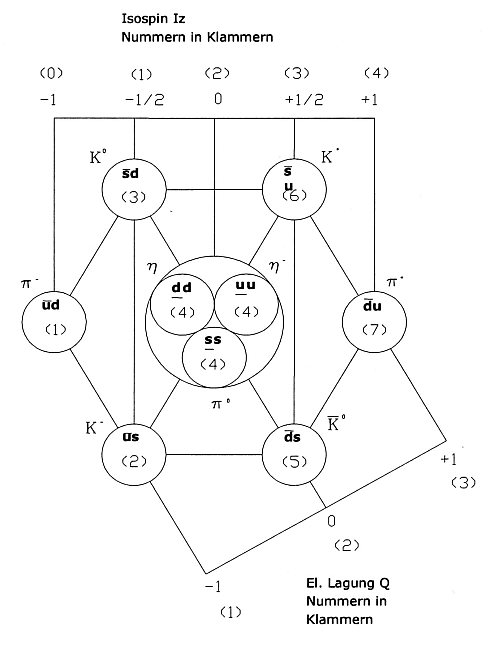
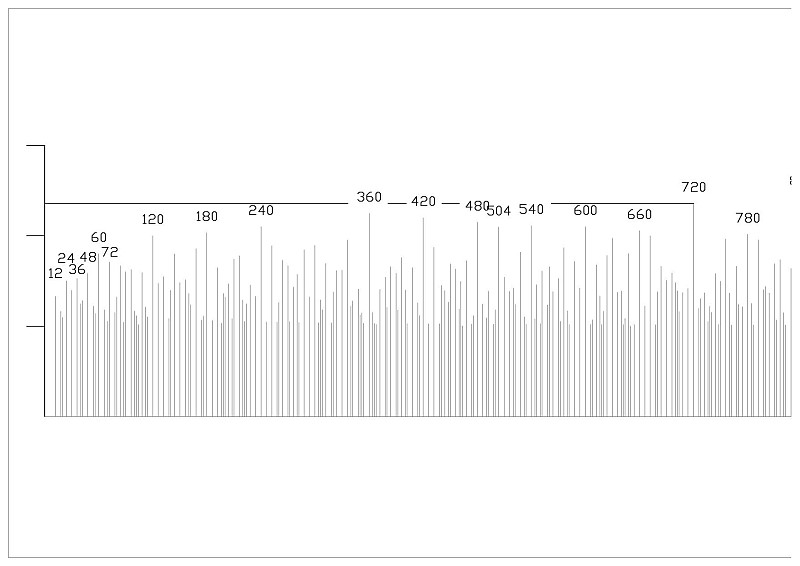
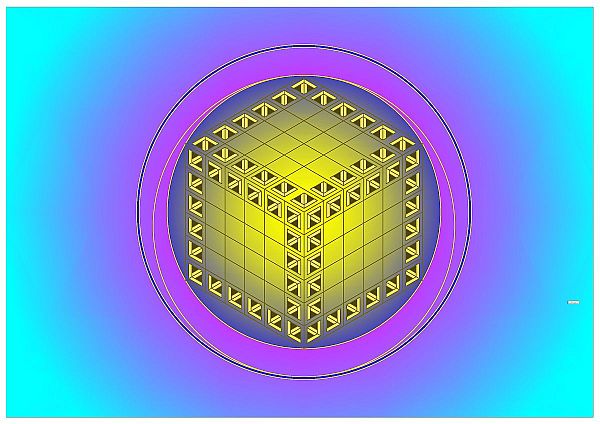
Mystik und Quantenphysik begegnen sich auf neue und unerwartete Weise. In der Tat bleiben solche Aussagen nicht im Ungefähren. Das Atom ist ein Hort ganz konkreter harmonikaler Zusammenhänge:

Harmonikale Betrachtungen über die modernen Vorstellungen vom Atom

Viele mystische Texte wie auch die Bilderwelt der Hermetik ist von Harmonik durchdrungen. Belege pythagoreischen Wissens sind in fast allen mystischen Bewegungen erkennbar. Viele Exempel finden wir bei Robert Fludd. Fludds „Himlisches Monochord“ wurde zum harmonikalen Aufmacher, ist jedoch geradezu eine Illustration zu Heisenbergs Zitat:

Ich habe allerdings noch tiefer greifende Betrachtungen angestellt, die zeigen, dass die mystischen Texte überraschende Erklärungen liefern, wenn wir sie richtig lesen:

Die Tabula Smaragdina Hermetis

Neue Auffassungen um das Herz als Organ

Jacob Böhme, Mysterium Pansophicum

Vollkommene Zahlen

Eine natürliche Zahl n wird vollkommene Zahl (auch perfekte Zahl) genannt, wenn sie gleich der Summe aller ihrer (positiven) Teiler außer sich selbst ist.
Wikipedia/Vollkommene Zahl

Das einfachste Beispiel: Die Zahl sechs hat drei Teiler 1, 2 und 3. Die Summe dieser Teiler ist 1+2+3 = 6. Die Zahl sechs ist also eine vollkommene Zahl. Die Summe der Teiler einer Zahl n wird mit Sigma σ*(n) bezeichnet. Es ist also: σ*(6) = 6. In Worten, die Teilersumme von sechs ist sechs.

σ(n): Oft wird als Teiler einer Zahl auch die Zahl selbst hinzugerechnet, dann heißt die Teilersumme σ(n). σ(n) = 1+2+3+6 = 12.Besonders schön ist nun, die Teiler zu Paaren zusammenzustellen: 2 x 3 = 1 x 6 = 6

Abundante Zahlen: Nicht jede Zahl ist eine vollkommene Zahl. σ*(12) = 1+2+3+4+6 = 16. Hier ist die Teilersumme größer als die Zahl selbst. Man nennt solche Zahlen Abundante Zahlen.

Defiziente Zahlen: Hingegen ist σ*(8) = 1+2+4 = 7. Zahlen, deren Teilersumme kleiner als die Zahl selbst ist, nennt man Defiziente Zahlen.

Die nächsten vollkommenen Zahl ist σ*(28) = 1+2+4+7+14 = 28. Die nächste vollkommene Zahl ist 496. -> Weitere Gesetzmäßigkeiten vollkommener Zahlen.

Harmonikale Aspekte an vollkommenen Zahlen. Ein Oberton ist dann besonders eingängig, wenn dieser möglichst viele Teiltöne besitzt. Der fünfte Oberton eines Grundtones klingt fremd, bzw. neu und ungewohnt, wenn man die Töne einzeln anspielt. Die Frequenzen 100 Hz, 200 Hz, 300 Hz und 400 Hz klingen noch besonders harmonisch und eingängig. Es finden sich die Frequenzverhältnisse Oktaven (1:2:4) und Quinte (2:3) vor. Der fünfte Oberton mit 500 Hz klingt neu, im Vergleich mit den vorhergehenden ungewohnt. Die große Terz mit dem Frequenzverhältnis 4:5 ist neu, da die Teilbarkeit der Zahl fünf gering ist. Fünf ist überdies eine Primzahl. Die Teilersumme σ*(5) = 1.

Musikalisch bewegen sich die Intervalle Oktave und Quinte in der Pentatonik. Musikhistorisch ist das Auftreten der Große Terz, etwa mit der Renaissance eine Zäsur. Mit dem Auftreten der Terzen beginnt die Musik des Quinten-Terzen-Systems, in dem wir noch heute musizieren.Septimen sind keine Naturseptimen mit den Frequenzverhältnissen 6:7:8, sondern sie sind eingebunden im Quinten-Terzen-System, etwa als diatonische Septime H in den leiterneigenen Dreiklang G-H-D (große Terz + kleine Terz, Frequenzverhältnis 4:5:6).

Die erste vollkommene Zahl sechs spielt eine herausragende Rolle in der Harmonik von Hans Kayser. Er nannte die ersten Intervalle der Frequenzverhältnisse 1:2:3:4:5:6, Senarius. Kayser meinte es seien die harmonisch klingenden Intervalle, während die Septime 6:7 disharmonisch sei. Hört man sich jedoch 6:7:8 an, oder etwa 5:6:7, so klingt dies ebenfalls harmonisch (Harmonienlehre nach Johannes Kotschy).

Der Senarius (1:2:3:4:5:6) hat indessen noch andere Qualitäten. Er enthält alle harmonisch klingenden und konstituierenden Intervalle des Quinten-Terzen-Systems. Die Frequenzproportionen 1:2:3:4, getrennt angeschrieben 1:1, 1:2, 2:3, 3:4, auf gemeinsamen Nenner gebracht (6:12, 8:12, 9:12, 12:12) und geordnet, bilden die Harmonia perfekta maxima (6,8,9,12), die Tonfolgen C – F – G – C‘, (Tonika-Dominante-Subdominante-Tonika), die Grundkadenz. Über die Tonstufen gelegter Dreiklang (Frequenzproportion 4:5:6), ergibt die vollständige diatonische Tonleiter.

Die hexagonale Geometrie des Senarius als eine Grundstruktur der Welt. Das regelmäßige Polygon mit sieben Ecken ist mit Zirkel und Lineal nicht konstruierbar, somit sind auch die Winkelfunktionen der Siebenerteilung des Kreises keine rationalen, sondern transzendente Zahlen. Insofern bildet die Sieben eine natürliche Grenze in den Symmetriebetrachtungen des Kreises. Dem entspricht das Quintenterzensystem mit seinen konstituierenden Intervallen (1:2:3:4:5:6), ohne dass dies von den Musiktheoretikern beabsichtigt war.  Unserer Musik, die wir etwa ab der Aufklärung betreiben, bewegt sich in diesem Rahmen unterhalb der Sieben. Das Hexagon birgt die Sieben in seiner Mitte, gewissermaßen ungeoffenbart, verborgen.

(Abbildung aus Limbrunner, Willibald; Zahl Seele Kosmos; Synergiea Verlag; 2010; Abb. 63.)

Ja sogar die Quantenphysik entdeckte mit den Symmetrien der Quarks die Hexagonalstruktur als eine grundlegende Symmetrie der schweren Teilchen. Also jenen Teilchen, welche u.a. den Atomkern bilden. Die obenstehende Abbildung zeigt die Symmetrien der Baryonen und Mesonen.

 

Teilersummen bis 720, siehe Abbildung oben: Die Vielfachen von zwölf (12, 24, 36, 48 …) haben besonders große Teilersummen σ*. Die Zahl Zwölf besitzt besonders viele Teiler (1,2,3,4,6). Erst mit der Zahl 60 und ihren Vielfachen werden die Teilersummen noch einmal erheblich größer. 60 ist die erste Vielfache von 12 die ebenfalls durch 5 teilbar ist. 60 ist eine besonders gut teilbare Zahl. Mit der Zahl 60 treten die Dreiklänge des Quinten-Terzen-Systems auf:
(1/4 : 1/5 : 1/6 = 15/60 : 12:60 : 10/60), KgV {4, 5, 6} = 60.
Die Zahl 720 = 1 x 2 x 3 x 4 x 5 x 6 überragt wiederum alle vorhergehenden Teilersummen.

Die Zahl 5040: Die im Platons Staat (Politeia) vorkommende Zahl 5040 = 1 x 2 x 3 x 4 x 5 x 6 x 7. als optimale Zahl an Menschen die in einen idealen Staat leben, überragt wiederum alle vorhergehenden. Mit dieser Zahl tritt die Sieben hinzu.

Zahl und Harmonik: Es sind also vollkommene und abundante Zahlen, die besonders viele Teiler haben, als Obertöne besonders eingängig, enthalten viele Teiltöne, wodurch sie stark mit ihren Teiltönen resonieren und klingen. Auf diese Weise kann man sehen, wie elementare Zahlentheorie und Harmonik zusammenwirken. Das Zitat aus den Hörsprüchen des Pythagoras zeigt an diesem Beispiel seine konkrete Bedeutung:

Was ist das Weiseste? Zahl

 

Die Zahl 72: Nicht alle Zahlen sind gleich, jede hat ihre Besonderheit. Herausragend bei den Teilersummen ist die Zahl 72. Im Zahlenraum 1 bis 6000 hat die Zahl 72 die größte Teilersummenhäufigkeit. D. h. sie kommt am häufigsten als Teilersumme in den Zahlen 1 bis 6000 vor. Beispiel:
30 = 1×30, 2×15, 3×10, 5×6      σ(30) = 72
46 = 1×46, 2×23                        σ(30) = 72
30 und 46 haben die gleiche Teilersumme 72. Die Zahl selbst wird als Teiler mitgerechnet σ(n).

Die Zahl 72 hat die Teiler 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72. Die fett markierten Zahlen enthalten beide Formen der für die Pythagoreer heiligen Tetraktys (1,2,3,4), (6,8,9,12). Letztere Form wurde vom römischen Philosophen und Schriftsteller Boetius als „Harmonia perfecta maxima“ bezeichnet. Siehe dazu auch: Kramer, Anton; Rationale und irrationale Harmonie, S.77

Die Zahlen 6 und 72 im Kubus. Oberfläche und Volumen bei einen Kubus mit der Kantenlänge sechs sind gleich. (O = V = 6 x 6 x 6 = 216) Es gibt nur einen einzigen ganzzahligen Wert der Kantenlänge, bei dem dies der Fall ist. Die Gesamtlänge aller 12 Kanten beträgt 72. 

W. Limbrunner, 2.11.2017